FICK'S FIRST AND SECOND LAWS

 

Fick's First Law states that 'the rate of "diffusion (e.g. of a vapour) is proportional to the surface area and the concentration difference, it is inversely proportional to the thickness of the membrane".

This means that the amount of gas transferred per unit time across a membrane is proportional to the area available for exchange and the partial pressure difference of the gas across the membrane. The constant of proportionality (K) is called the-diffusion coefficient. This is the same as saying that the vapour flows from regions of high concentration to regions of low concentration, and the amount that flows is proportional to the concentration gradient across the membrane

The law can be expressed mathematically in many forms, including :-

where

• J is the diffusion flux. J is the amount of substance (vapour) that flows through a unit area (e.g. per square cm) of a barrier or sample per unit time (e.g. per second)
• D is the diffusion coefficient.
• φ (for ideal mixtures) is the concentration, or the amount of substance per unit volume.
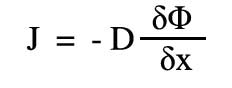
• x is effectively the width of the membrane

Alternatively it can be expressed as

 

 

Where:

• Delta N is the mass of vapour transfered
• Delta t is time
• A is the area of the sample
• Delta P is the partial pressure of the vapour
• K is Krogh's diffusion coefficient, this is slightly different to the diffusion constant (K = aD) which is the diffusion coefficient (D) times the solubility (a) of a gas in the fluid through which the gas diffuses

How accurate and how valid is Fick's First law?

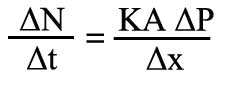
Fick’s law was developed empirically rather than theoretically, however it is very precise in normal use because simply because molecules are very small vapours can be considered as continuous rather than statistical, even in cases where the volumes of the vapours are minute.

However Fick can only be applied to systems that are in a steady state and the system is in unchanging. However, measurements can be facilitated by factors that do not effect Fick's law - such as convection air currents, that assist in spreading particles and sweeping them past sensors.

In situations where situations are changing, for example while pressures are being brought into balance, Fick's Second law can be applied.

 

Fick's Second law

Fick's 2nd law of diffusion states that the rate of accumulation (or depletion) of concentration within the volume is proportional to the local curvature of the concentration gradient.

It is expressed mathematically as a partial differential equation:-

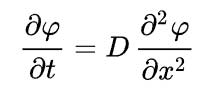
where

• φ is the concentration
• φ = φ(x,t) is a function that changes over position x and time t
• t is time
• D is the diffusion coefficient
• x is the position (thickness)

In two or more dimensions the Laplacian Δ = ∇2, is required to generalises the second derivative leading to

 

What is vapour permeability?

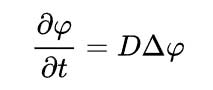
The you tube video ( https://www.youtube.com/watch?v=iOHFrtCxAxc&t=2s )+ is useful in explainning Fick's law made by Texas A&M: Intro to Materials. It is relevant to all fluids such as liquids and gases / vapours.